算法问题

1.两数求和：哈希映射

使用hashmap来实现，key里放要判别的数，value里放下标

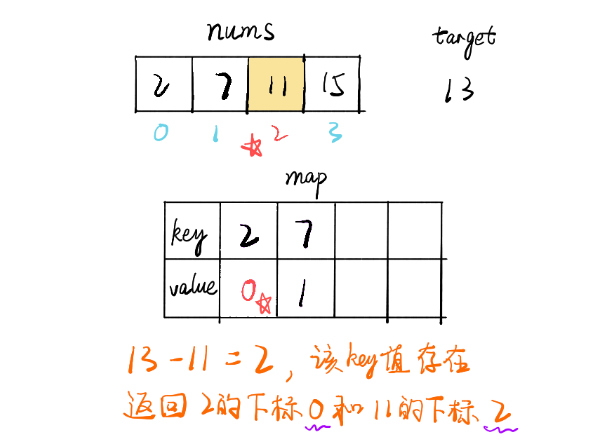
class Solution {
    public int[] twoSum(int[] nums, int target) {
        HashMap<Integer,Integer> map=new HashMap<>();
        for(int i=0;i<nums.length;i++){
            if(map.containsKey(target-nums[i])){
                return new int[] {map.get(target-nums[i]),i};
            }
            map.put(nums[i],i);
        }
        throw new IllegalArgumentException("No two sum solution");
    }
}

2.判断子序列：双指针

使用上下双指针，charAt()方法

class Solution {
    public boolean isSubsequence(String s, String t) {
        if(s.length()==0){
            return true;
        }
        for(int i=0,j=0;j<t.length();j++){
            if(s.charAt(i)==t.charAt(j)){
                i++;
                if(i==s.length()){
                    return true;
                }
            }
        }
        return false;
    }
}

3.回文数：字符串反转(慢) 双指针(略慢) 数字处理/%(快)

要先排除负数，121是回文数

字符串反转：

class Solution {
    public boolean isPalindrome(int x) {
        if(x<0){
            return false;
        }
        StringBuilder zheng = new StringBuilder(x+"");
        StringBuilder fan=new StringBuilder(zheng).reverse();//注意
        if(zheng.toString().equals(fan.toString())){
            return true;
        }else{
            return false;
        }
    }
}
//优化(别人写的比我简洁多了)
class Solution {
    public boolean isPalindrome(int x) {
        if(x<0) return false;
        String s = x + "";
        StringBuilder n = new StringBuilder(s);
        return n.reverse().toString().equals(s);
    }
}

双指针：

class Solution {
    public boolean isPalindrome(int x) {
        String str=x+"";
        int left=0;
        int right=str.length()-1;
        while(left<right){
            if(str.charAt(left)==str.charAt(right)){
                left++;
                right--;
            }else{
                return false;
            }
        }
        return true;
    }
}

数字处理：

class Solution {//自己真想不到吧
    public boolean isPalindrome(int x) {
        if(x < 0)
            return false;
        int cur = 0;
        int num = x;
        while(num != 0) {
            cur = cur * 10 + num % 10;
            num /= 10;
        }
        return cur == x;
    }
}

4.加一：数学解题%

题目：

//写出这个代码的人简直就是天才，我五体投地了。太特么聪明了
class Solution {
    public int[] plusOne(int[] digits) {
        for (int i = digits.length - 1; i >= 0; i--) {
            digits[i]++;
            digits[i] = digits[i] % 10;
            if (digits[i] != 0) return digits;
        }
        digits = new int[digits.length + 1];
        digits[0] = 1;
        return digits;
    }
}

5.爬楼梯：斐波那契数列(递归+hashmap，循环)

题目：

思路：其实就是斐波那契数列，比如一共n层，若第一步走1层，f(n-1)为后面n-1层的所有方法数，若第一步走2层，f(n-2)

为后面n-2层方法数，以此类推递归，直到后面只剩1层就只有1种方法了，只剩两层就只有2种方法了

但是直接递归大概率会超时，我们需要借助hashmap存储我们算过的f(n)防止重复计算

当然所有递归都可以改用循环代替

单纯递归（超时了）：

class Solution {
    public int climbStairs(int n) {
        if(n==1) return 1;
        if(n==2) return 2;
        return climbStairs(n-1)+climbStairs(n-2);;
    }
}

递归+hashmap：

class Solution {
    private HashMap<Integer,Integer> map=new HashMap<>();
    public int climbStairs(int n) {
        if(n==1) return 1;
        if(n==2) return 2;
        if(map.containsKey(n)){
            return map.get(n);
        }
        int result = climbStairs(n-1)+climbStairs(n-2);
        map.put(n,result);
        return result;
    }
}

循环：

class Solution {//纯纯斐波那契数列啊：1+2+3+5+8+...
    public int climbStairs(int n) {
        if(n==1) return 1;
        if(n==2) return 2;
        int start=1;
        int end=2;
        int result=0;
        for(int i=2;i<n;i++){
            result = start+end;
            start=end;
            end=result;
        }
        return result;
    }
}

6.合并两个有序数组：双指针

题目：

解题：

sort()方法，直接拼接两个数组然后使用Arrays.sort():

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        for(int i=0;i<n;i++){
            nums1[m+i]=nums2[i];
        }
        Arrays.sort(nums1);
    }
}

双指针(头):

//注意点：如果数组1或2提前全部排序完了，那就直接把剩下的另一个数组的数字依次加到后面就行
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int pt1=0;
        int pt2=0;
        int i=0;
        int[] result=new int[m+n];
        while(pt1<m || pt2<n){
            if(pt1>=m && pt2<n){
                result[i]=nums2[pt2++];
                i++;
                continue;
            }
            if(pt1<m && pt2>=n){
                result[i]=nums1[pt1++];
                i++;
                continue;
            } 
            if(nums1[pt1]<nums2[pt2]){
                result[i]=nums1[pt1++];
                i++;
            }else{
                result[i]=nums2[pt2++];
                i++;
            }
        }
        for(int j=0;j<m+n;j++){
            nums1[j]=result[j];
        }
    }
}
//这个方法弊端就是需要额外创建一个数组，最后还要从新把数组赋值给nums1，于是有了下面的这种双指针方法（从尾部往前判断）

双指针(尾)：

class Solution {//虽然但是，我自己写的时候都懵懵的，还是上面那种好写一点，这种方法空间复杂度好像也没少多少
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int pr1=m-1;
        int pr2=n-1;
        int index=m+n-1;
        while(index>=0){
            if(pr1<0){
                nums1[index--]=nums2[pr2--];
                continue;
            }
            if(pr2<0){
                break;
            }
            if(nums1[pr1]>nums2[pr2]){
                nums1[index--]=nums1[pr1--];
            }else{
                nums1[index--]=nums2[pr2--];
            }
        }
    }
}

7.移动零：双指针

题目：

解题：

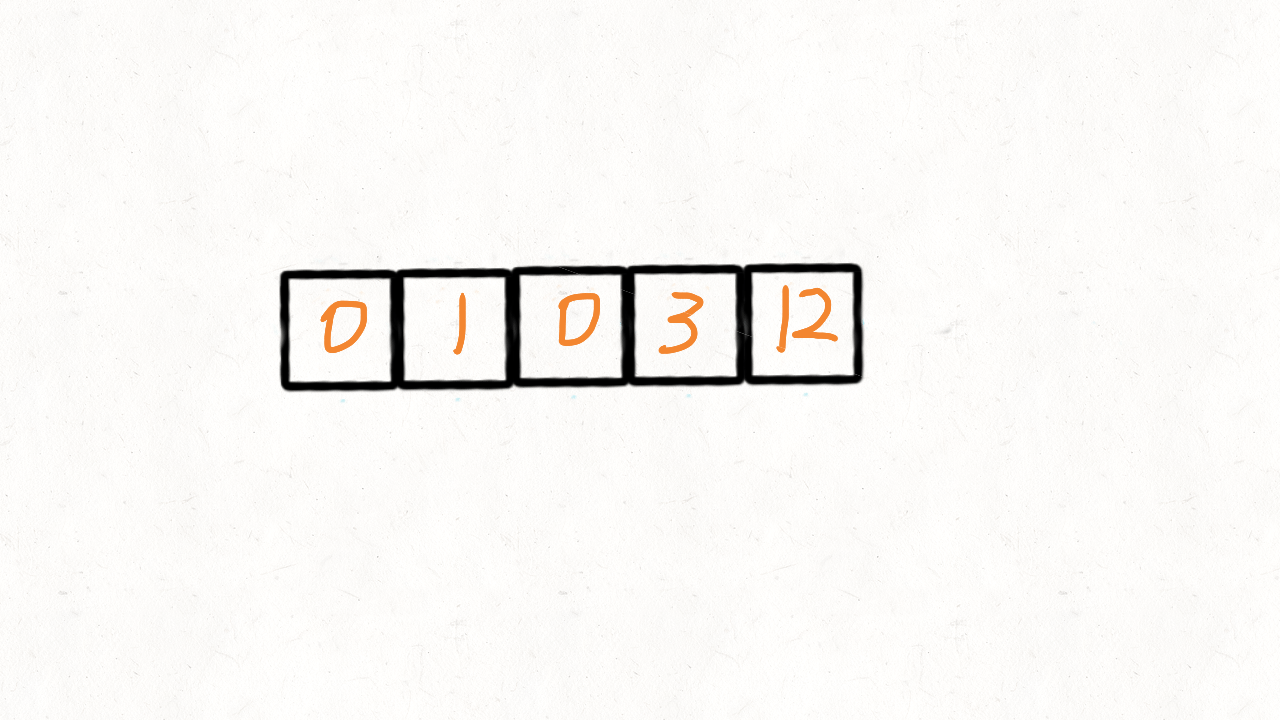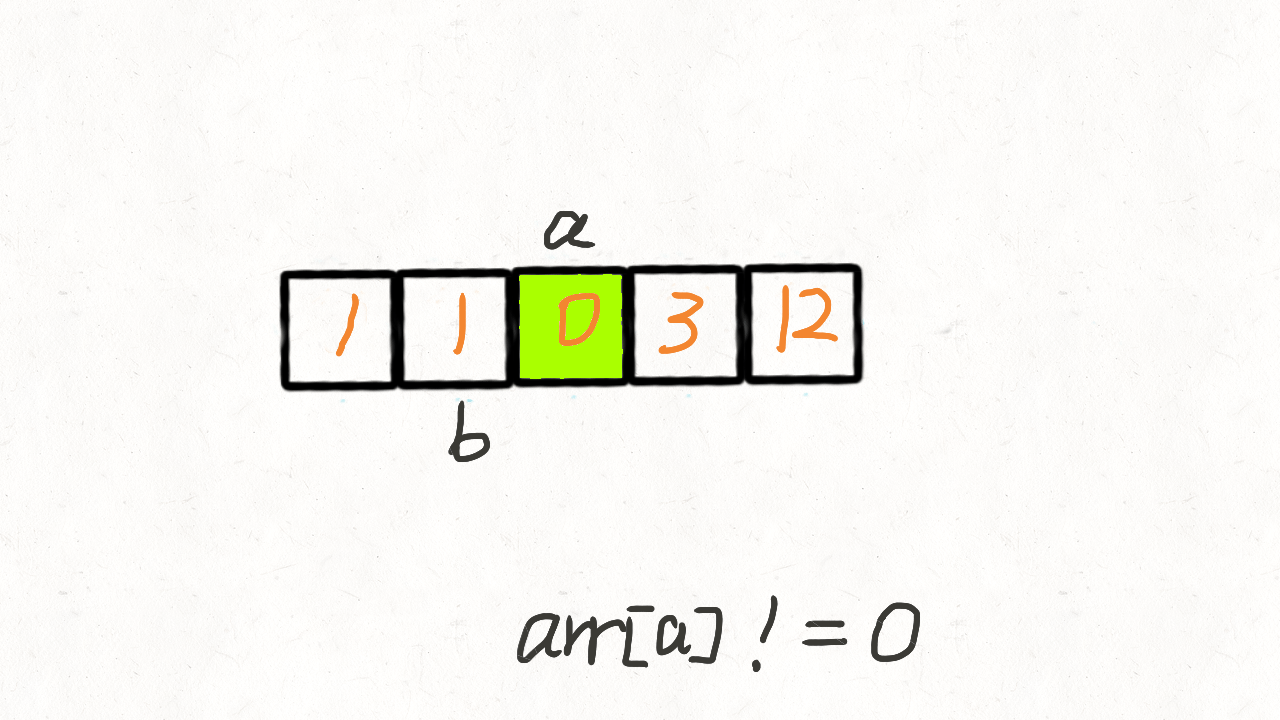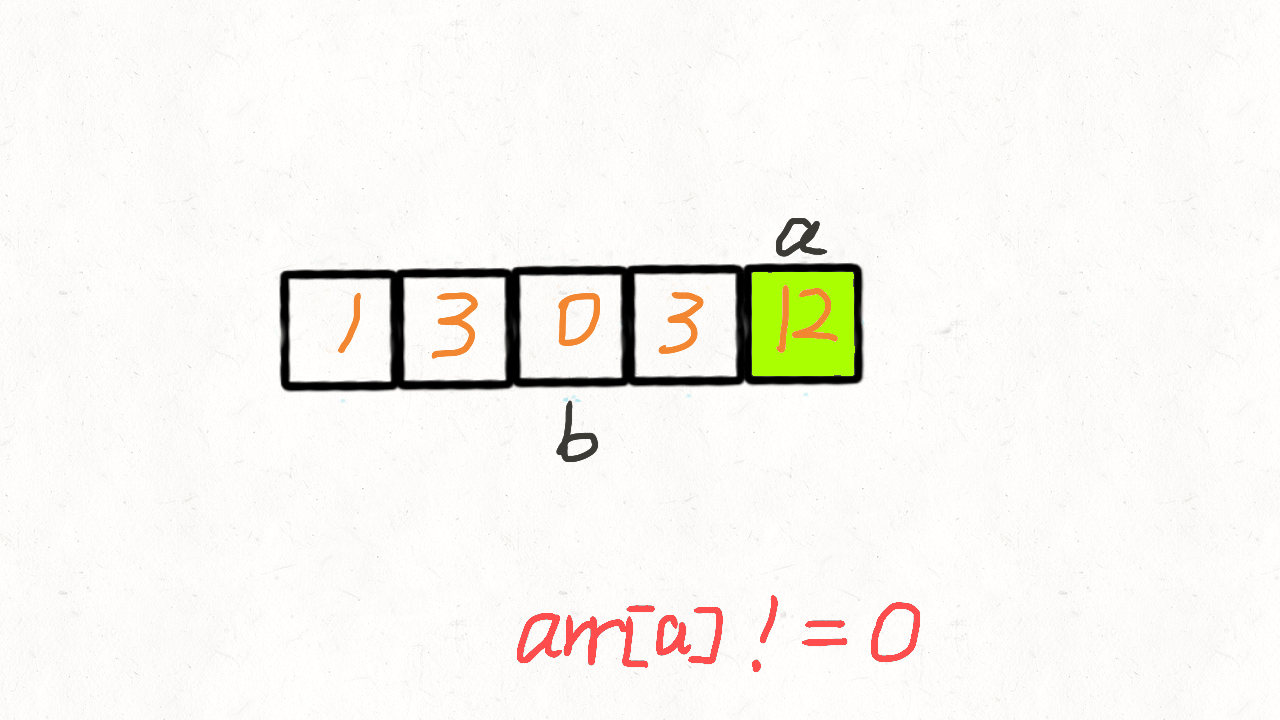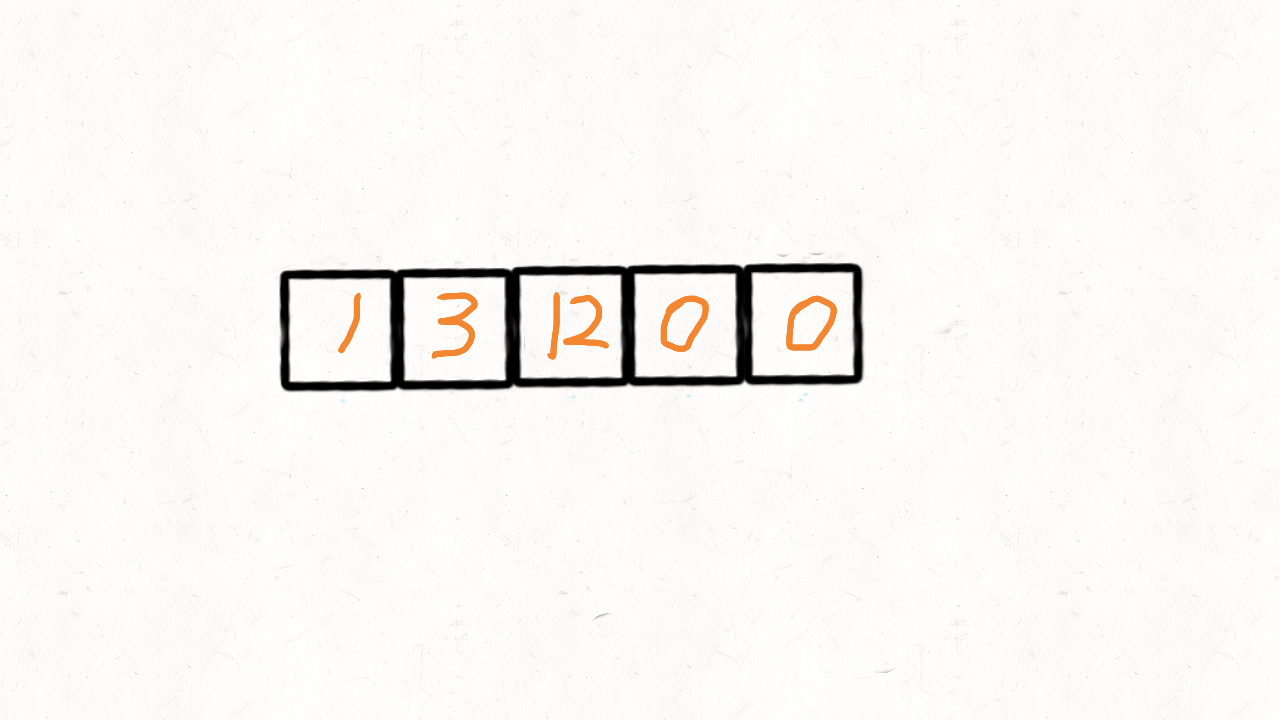
双指针：

class Solution {
    public void moveZeroes(int[] nums) {
        int j=0;
        for(int i=0;i<nums.length;i++){
            if(nums[i]!=0){
                nums[j++]=nums[i];
            }
        }
        for(int i=j;i<nums.length;i++){
            nums[i]=0;
        }
    }
}

8.找到所有数组中消失的数字：

要求：不使用额外空间，时间复杂度O(n)

题目:

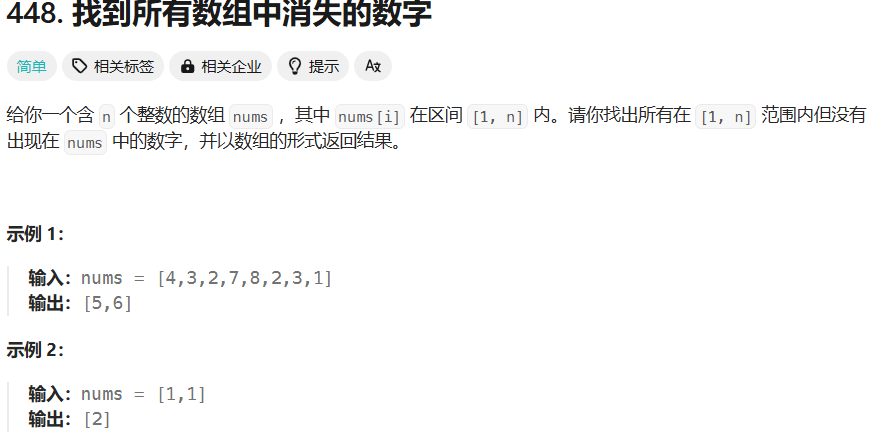
解题：

将数组放到他理应在的位置上：

class Solution {//看不明白，太难了这题，到最后都没明白
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer> res = new ArrayList<>();
        int i = 0;
        while (i < nums.length) {
            if (nums[i] == i + 1) {
                i++;
                continue;
            }
            int idealIdx = nums[i] - 1;
            if (nums[i] == nums[idealIdx]) {
                i++;
                continue;
            }
            int tmp = nums[i];
            nums[i] = nums[idealIdx];
            nums[idealIdx] = tmp;
        }
        for (int j = 0; j < nums.length; j++) {
            if (nums[j] != j + 1) {
                res.add(j + 1);
            }
        }
        return res;
    }
}

最快答案：(也没看懂)

class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer> res = new LinkedList<>();
        int n = nums.length;
       for(int num: nums){
           nums[(num -1)%n] += n;
       }
       for(int i = 0; i < n; i++){
        //少的数在角标中找加一
        if(nums[i] <= n)res.add(i+1);
       }
        return res;
    }
}

9.合并两有序链表：双指针，递归

双指针：

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        if(list1==null) return list2;
        if(list2==null) return list1;
        ListNode result=new ListNode(0);
        ListNode p=result;
        while(list1!=null && list2!=null){
            if(list1.val>list2.val){
                p.next=list2;
                list2=list2.next;
            }else{
                p.next=list1;
                list1=list1.next;
            }
            p=p.next;
        }
        if(list1==null){
            p.next=list2;
        }
        if(list2==null){
            p.next=list1;
        }
        return result.next;
    }
}

递归：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
//就是将大问题分为相同的小问题，就使用递归
class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        if(list1==null) return list2;
        if(list2==null) return list1;
        if(list1.val>list2.val){
            list2.next=mergeTwoLists(list1,list2.next);
            return list2;
        }else{
            list1.next=mergeTwoLists(list1.next,list2);
            return list1;
        }
        
    }
}

10.删除排序链表中的重复元素：正常遍历和递归

太简单了

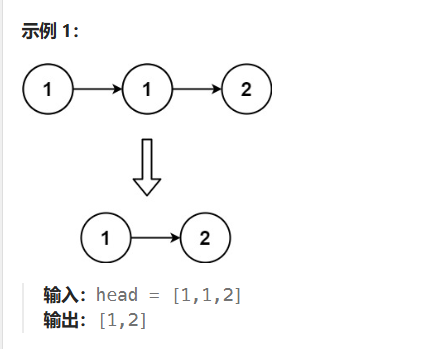
解题：

正常遍历：

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if(head==null){
            return head;
        }
        if(head.next==null){
            return head;
        }
        ListNode currentNode=head;
        while(currentNode.next!=null){
            if(currentNode.next.val==currentNode.val){
                currentNode.next=currentNode.next.next;
            }else{
                currentNode=currentNode.next;
            }
        }
        return head;
    }
}

递归：

大问题可以分成很多相同的小问题解决

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if(head==null){
            return head;
        }
        if(head.next==null){
            return head;
        }
        if(head.next.val==head.val){
            head.next=deleteDuplicates(head.next);
            return head.next;
        }
        else{
            head.next=deleteDuplicates(head.next);
            return head;
        }
        
    }
}

11.环形链表：快慢指针

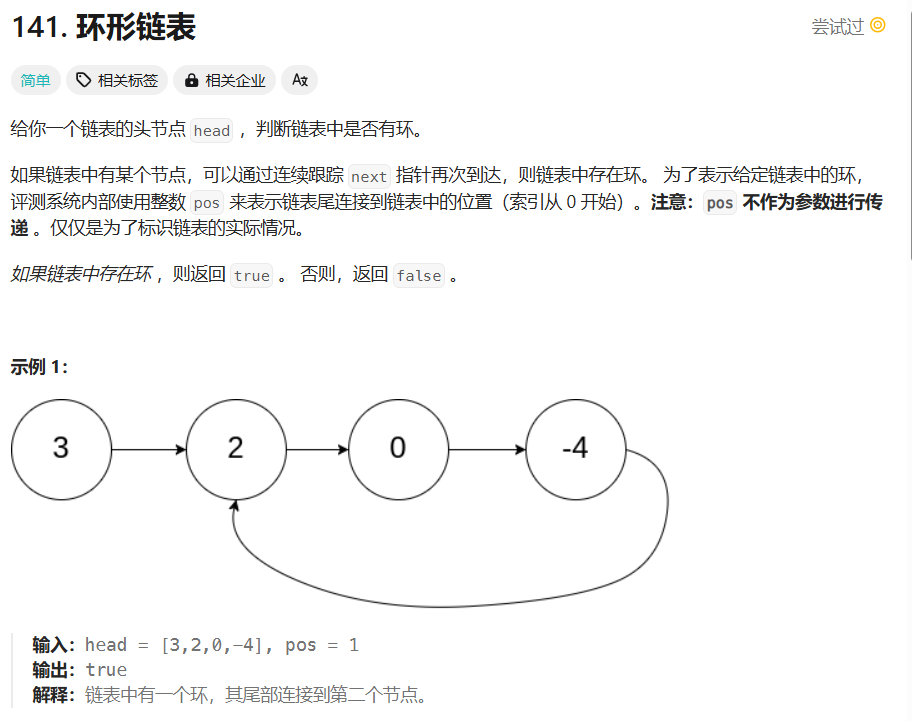
解题：

思路：快指针一次2步，慢指针一次1步

若有环路，快指针肯定会追上慢指针重合，若无环路，则快指针会到链表末尾null

快慢指针：

public class Solution {
    public boolean hasCycle(ListNode head) {
        if(head==null || head.next==null) return false;
        ListNode fast=head;
        ListNode slow=head;
        while(fast.next!=null && fast.next.next!=null){
            fast=fast.next.next;
            slow=slow.next;
            if(fast==slow){
                return true;
            }
        }
        return false;
    }
}

12.环形链表2 ：快慢指针

环形链表的进阶，不仅要判断链表是否有环，有环时还要返回从哪个节点开始有环的

解题思路：

前面判断有环和原本快慢指针一样，当快慢指针指到一起时判断为有环，然后将慢指针放到链表头部，快指针不动但变为和慢指针一样的速度，然后同时往后移动，当两个指针再次相遇时的节点就是环入口节点。

先快慢指针，后速度一致：

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if(head==null || head.next==null){
            return null;
        }
        ListNode fast=head;
        ListNode slow=head;
        boolean isCycle=false;
        while(fast.next!=null && fast.next.next!=null){
            fast=fast.next.next;
            slow=slow.next;
            if(fast==slow){
                isCycle=true;
                break;
            }
        }
        if(isCycle==true){
            slow=head;
            while(slow!=fast){
                slow=slow.next;
                fast=fast.next;
            }
            return slow;
        }
        return null;
    }
}

13.相交链表：双指针交错遍历

题目：

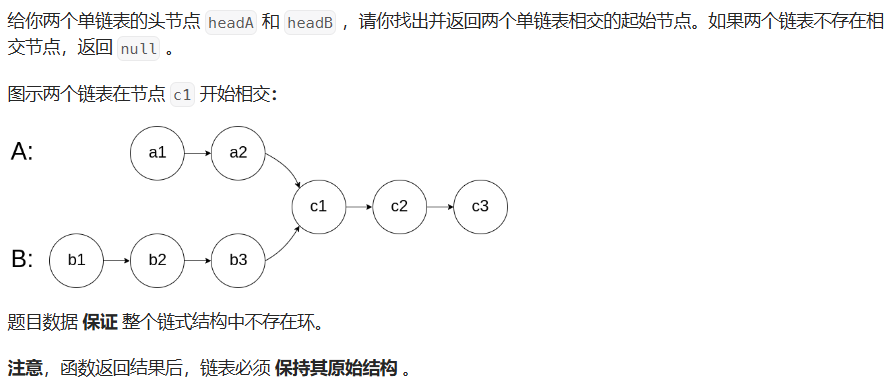
思路：

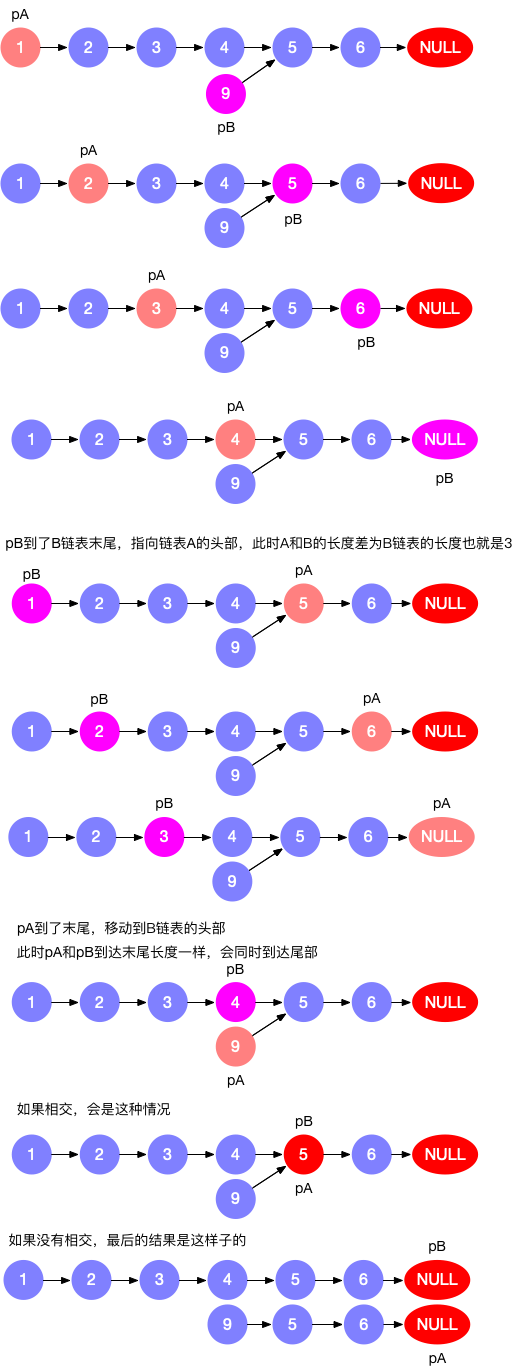
解题：

双指针交错遍历：

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if(headA==null) return null;
        if(headB==null) return null;
        ListNode p1=headA;
        ListNode p2=headB;
        while(p1!=p2){
            p1=(p1==null?headB:p1.next);
            p2=(p2==null?headA:p2.next);
        }
        return p1;
    }
}

14.反转链表：双指针

两个指针，per指向当前节点前一个节点(初始为null) cur节点指向当前节点，同时每次遍历前都要记录当前节点的下一个节点

双指针：

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre= null;
        ListNode cur=head;
        while(cur!=null){
            ListNode nextNode=cur.next;
            cur.next=pre;
            pre=cur;
            cur=nextNode;
        }
        return pre;
    }
}

15.回文链表：快慢指针+反转链表

思路：

快慢指针来遍历，快指针遍历到尾巴后，慢指针正好在链表中间，分奇数偶数情况，偶数的话快指针最后为null，奇数的话快指针最后的next为null，以此来区分奇数偶数，如果为奇数，慢指针还需要向后挪一位，然后反转慢指针后面的一段链表，快指针再重新指向整个链表头部，然后快慢指针同速度往下比较，若有不同则表示不是回文链表，慢指针为null时结束

快慢指针+反转链表：

class Solution {
    public boolean isPalindrome(ListNode head) {
        if(head==null) return false;
        if(head.next==null) return true;
        ListNode fast=head;
        ListNode slow=head;
        while(fast!=null && fast.next!=null){
            slow=slow.next;
            fast=fast.next.next;
        }
        if(fast!=null){
            slow=slow.next;
        }
        fast=head;
        slow=reserveNode(slow);
        while(slow!=null){
            if(slow.val!=fast.val){
                return false;
            }
            slow=slow.next;
            fast=fast.next;
        }
        return true;
    }
    public ListNode reserveNode(ListNode head) {
        if(head.next==null){
            return head;
        }
        ListNode per=null;
        ListNode cur=head;
        while(cur!=null){
            ListNode nextNode=cur.next;
            cur.next=per;
            per=cur;
            cur=nextNode;
        }
        return per;
    }
}

16.链表的中间节点：快慢指针

快慢指针：

class Solution {
    public ListNode middleNode(ListNode head) {
        if(head==null) return null;
        ListNode fast=head;
        ListNode slow=head;
        while(fast!=null && fast.next!=null){
            fast=fast.next.next;
            slow=slow.next;
        }
        return slow;
    }
}

17.链表中倒数第k个节点：双指针前后指针

思路：

前面的指针先往后移k-1位，然后前后指针同时往后一步一步移动，前指针为null时，后指针所指向的节点就是倒数第k个节点

双指针前后指针：

class Solution {
    public int kthToLast(ListNode head, int k) {
        ListNode fast=head;
        ListNode slow=head;
        while(k-1>=0){
            k--;
            fast=fast.next;
        }
        while(fast!=null){
            fast=fast.next;
            slow=slow.next;
        }
        return slow.val;
    }
}

18.找出与数组相加的整数1：最小值之差

题目：

思路：

拿到nums1和nums2的最小值，之差就是答案

最小值之差：

class Solution {
    public int addedInteger(int[] nums1, int[] nums2) {
        int n1=min(nums1);
        int n2=min(nums2);
        return n2-n1;
    }
    private int min(int[] nums){
        int res=Integer.MAX_VALUE;
        for(int num : nums){
            res=Math.min(res,num);
        }
        return res;
    }
}

19.用栈模拟队列：两个栈

题目：

思路：

push到第一个栈中，pop是从第二个栈中pop，如果第二个栈为空就把第一个栈的元素pop出来push到第二个栈再pop出来，先进后出+先进后出=先进先出

两个栈：

class MyQueue {

    private Stack<Integer> A;
    private Stack<Integer> B;

    public MyQueue() {
        A=new Stack<>();
        B=new Stack<>();
    }
    
    public void push(int x) {
        A.push(x);
    }
    
    public int pop() {
        if(B.isEmpty()){
            while(!A.isEmpty()){
                B.push(A.pop());
            }
        }
        return B.pop();
    }
    
    public int peek() {
        if(B.isEmpty()){
            while(!A.isEmpty()){
                B.push(A.pop());
            }
        }
        return B.peek();
    }
    
    public boolean empty() {
        if(A.isEmpty() && B.isEmpty()){
            return true;
        }
        else{
            return false;
        }
    }
}

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * boolean param_4 = obj.empty();
 */

20.字符串解码：栈

题目：

地址：

394. 字符串解码 - 力扣（LeetCode）

答案：

栈：

class Solution {
    int ptr;

    public String decodeString(String s) {
        LinkedList<String> stk = new LinkedList<String>();
        ptr = 0;

        while (ptr < s.length()) {
            char cur = s.charAt(ptr);
            if (Character.isDigit(cur)) {
                // 获取一个数字并进栈
                String digits = getDigits(s);
                stk.addLast(digits);
            } else if (Character.isLetter(cur) || cur == '[') {
                // 获取一个字母并进栈
                stk.addLast(String.valueOf(s.charAt(ptr++))); 
            } else {
                ++ptr;
                LinkedList<String> sub = new LinkedList<String>();
                while (!"[".equals(stk.peekLast())) {
                    sub.addLast(stk.removeLast());
                }
                Collections.reverse(sub);
                // 左括号出栈
                stk.removeLast();
                // 此时栈顶为当前 sub 对应的字符串应该出现的次数
                int repTime = Integer.parseInt(stk.removeLast());
                StringBuffer t = new StringBuffer();
                String o = getString(sub);
                // 构造字符串
                while (repTime-- > 0) {
                    t.append(o);
                }
                // 将构造好的字符串入栈
                stk.addLast(t.toString());
            }
        }

        return getString(stk);
    }

    public String getDigits(String s) {
        StringBuffer ret = new StringBuffer();
        while (Character.isDigit(s.charAt(ptr))) {
            ret.append(s.charAt(ptr++));
        }
        return ret.toString();
    }

    public String getString(LinkedList<String> v) {
        StringBuffer ret = new StringBuffer();
        for (String s : v) {
            ret.append(s);
        }
        return ret.toString();
    }
}

21.二叉树中序遍历：递归

题目：

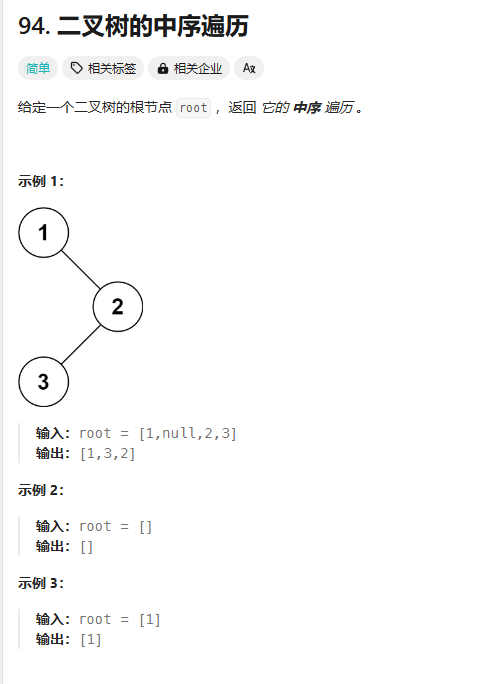
中序遍历：

class Solution {
    List<Integer> list=new ArrayList<Integer>(); 
    public List<Integer> inorderTraversal(TreeNode root) {
        if(root==null){
            return list;
        }
        doTree(root);
        return list;
    }
    private void doTree(TreeNode node){
        if(node==null){
            return;
        }
        doTree(node.left);
        list.add(node.val);
        doTree(node.right);
    }
}

22.二叉树前序遍历：递归

class Solution {
    List<Integer> list=new ArrayList<Integer>();
    public List<Integer> preorderTraversal(TreeNode root) {
        if(root==null){
            return list;
        }
        doTree(root);
        return list;
    }

    private void doTree(TreeNode node){
        if(node==null){
            return;
        }
        list.add(node.val);
        doTree(node.left);
        doTree(node.right);
    }
}

23.二叉树后序遍历：递归

class Solution {
    List<Integer> list=new ArrayList<Integer>();
    public List<Integer> postorderTraversal(TreeNode root) {
        if(root==null){
            return list;
        }
        doTree(root);
        return list;
    }
        private void doTree(TreeNode node){
        if(node==null){
            return;
        }
        doTree(node.left);
        doTree(node.right);
        list.add(node.val);
    }
}

24.对称二叉树：递归

思路：

递归比较左节点的左节点和右节点的右节点是否相同，左节点的右节点和右节点的左节点是否相同，递归结束条件是看比较的两个节点都为null返回true，有一个为null那肯定不对称，若值不相等也不对称，以上都不满足则递归第一句的比较。

递归：

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root==null) return false;
        return deepTree(root.left,root.right);
    }

    private boolean deepTree(TreeNode left,TreeNode right){
        if(left==null && right==null){
            return true;
        }
        //若只有一个等于null，则必不对称
        if(left==null || right==null){
            return false;
        }
        if(left.val!=right.val){
            return false;
        }
        return deepTree(left.left,right.right) && deepTree(left.right,right.left);
    }
}

25.二叉树的最大深度：递归

递归：

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null) return 0;
        return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
    }
}

26.平衡二叉树：递归+最大深度

高度平衡二叉树定义:一个二叉树每个节点的左右两子树的高度差不能大于1

思路：

其实就是在最大深度的题目代码上改造，递归判断左右子树最大高数之差是否大于1，但凡中途有一个子树不是平衡二叉树，那么整棵树肯定不是平衡二叉树了，返回-1

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root==null) return true;
        return balanceTree(root)!=-1;
    }

    private int balanceTree(TreeNode node){
        if(node==null) return 0;
        int left=balanceTree(node.left);
        int right=balanceTree(node.right);
        if(left==-1 || right==-1 || Math.abs(left-right)>1){
            return -1;
        }
        return Math.max(left,right)+1;
    }
}

27.翻转二叉树：递归

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root==null) return null;
        invertTree(root.left);
        invertTree(root.right);
        TreeNode temp=root.left;
        root.left=root.right;
        root.right=temp;
        return root;
    }
}

特别篇：十大排序算法

1.冒泡排序

2.选择排序

冒泡排序和选择排序差不多，选择排序相当于冒泡的优化，只有选到最大的数再交换，减少了交换的次数

平均时间复杂度：O(n^2)

空间复杂度: O(1)

3.插入排序

插入排序对于部分有序的数组十分高效，也很适合小规模数组

对于大规模的乱序数组很慢

平均时间复杂度：O(n^2)

空间复杂度: O(1)

4.快速排序

使用分治法将原始数据分为较小的子集，并递归地对这些子集进行排序；

优点：正常情况下非常高效，时间:O(n log n) 空间:O(log n)

缺点：当要排序的数组本身就有序或者逆序或存在大量重复元素的时候，可能导致分区后的子数组长度与原数组长度几乎相同，时间复杂度退化为 O(n^2)

5.希尔排序

基于插入排序不稳定的排序算法

需要增量序列，没有指定最好的增量序列

希尔增量序列：{N/2,(N/2)/2......1}

Hibbard序列：{2^k-1,...,3,1}

6.归并排序

通过递归和分而治之实现

7.堆排序

8.计数排序

仅适用于待排序元素为整数，分布较连续，跨度小的情况

9.桶排序

10.基数排序

28.手撕快速排序：

刘梦杰自己写的：

public class QuickSort {
    public static void main(String[] args){
        int[] arr={10, 7, 8, 9, 1, 5};
        int n=arr.length;
        System.out.println("原数组：");
        for(int num:arr){
            System.out.print(num+" ");
        }
        quickSort(arr,0,n-1);
        System.out.println();
        System.out.println("排序后：");
        for(int num:arr){
            System.out.print(num+" ");
        }
    }

    private static void quickSort(int[] arr,int left,int right){
        if(left>=right) return;
        //选数组最右边的作为基准点
        int standPoint=arr[right];
        //分类下标(把数组分成做左右部分的中间下标)
        int index=left-1;
        //遍历下标
        int i=left;
        //遍历
        while (i<right){
            if(arr[i]<=standPoint){
                index++;
                if (index<i){
                    int temp=arr[i];
                    arr[i]=arr[index];
                    arr[index]=temp;
                }
            }
            i++;
        }
        index++;
        int temp=arr[right];
        arr[right]=arr[index];
        arr[index]=temp;
        quickSort(arr,left,index-1);
        quickSort(arr,index+1,right);
    }
}

网上的：

public class QuickSort {

    // 主方法，用于测试快速排序
    public static void main(String[] args) {
        int[] arr = {10, 7, 8, 9, 1, 5};
        int n = arr.length;

        System.out.println("Unsorted array: ");
        printArray(arr);

        quickSort(arr, 0, n - 1);

        System.out.println("\nSorted array: ");
        printArray(arr);
    }

    // 快速排序主方法
    public static void quickSort(int[] arr, int low, int high) {
        if (low < high) {
            // 获取分区索引
            int pi = partition(arr, low, high);

            // 对分区左侧和右侧分别进行快速排序
            quickSort(arr, low, pi - 1);
            quickSort(arr, pi + 1, high);
        }
    }

    // 分区方法
    public static int partition(int[] arr, int low, int high) {
        int pivot = arr[high];  // 选择最右边的元素作为基准点
        int i = (low - 1);  // 记录小于基准点的元素的索引

        for (int j = low; j < high; j++) {
            // 如果当前元素小于或等于基准点
            if (arr[j] <= pivot) {
                i++;

                // 交换 arr[i] 和 arr[j]
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }

        // 将基准点放到正确的位置上
        int temp = arr[i + 1];
        arr[i + 1] = arr[high];
        arr[high] = temp;

        return i + 1;
    }

    // 打印数组
    public static void printArray(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }
}

28.2 手撕归并排序：

class Solution {
    public int[] sortArray(int[] nums) {
        return sort(nums, 0, nums.length - 1);
    }

    private int[] sort(int[] nums, int left, int right) {
        if (right - left + 1 < 2) return new int[]{nums[left]};//重点注意
        int mid = (left + right) / 2;
        return merge(sort(nums, left, mid), sort(nums, mid + 1, right));
    }

    private int[] merge(int[] nums1, int[] nums2) {
        int i = 0, j = 0, k = 0;
        int[] result = new int[nums1.length + nums2.length];
        while (k < result.length) {
            if (i >= nums1.length) {
                result[k++] = nums2[j++];
            } else if (j >= nums2.length) {
                result[k++] = nums1[i++];
            } else if (nums1[i] <= nums2[j]) {
                result[k++] = nums1[i++];
            } else {
                result[k++] = nums2[j++];
            }
        }
        return result;
    }
}

29.二分查找：循环,递归

二分查找前提条件是需要查找的数组是有序的

循环：

class Solution {
    public int search(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        while(left<=right){
            int mid=(left+right)/2;
            if(nums[mid]>target){
                right=mid-1;//注意:需要mid-1
            }else if(nums[mid]<target){
                left=mid+1;//注意:需要mid+1
            }else if(nums[mid]==target){
                return mid;
            }
        }
        return -1;
    }
}

递归：

class Solution {
    public int search(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        return doSearch(left,right,nums,target);
    }

    private int doSearch(int left,int right,int[] nums,int target){
        if(left>right){
            return -1;
        }
        int mid=(left+right)/2;
        if(nums[mid]>target){
            return doSearch(left,mid-1,nums,target);
        }else if(nums[mid]<target){
            return doSearch(mid+1,right,nums,target);
        }else{
            return mid;
        }
    }
}

特别篇：原码反码补码和位运算

正数的原码反码补码都是一样的，

负数的反码为源码取反(符号位除外)

负数的补码为反码+1

位运算：

按位与 &

按位或 |

按位非 ~

按位异或 ^

有符号右移 >>（正数高位补0，负数高位补1）

有符号左移 <<

无符号右移 >>>（无论正负，高位都补0）

两数交换：

a=1,b=3
a=a+b;
b=a-b;
a=a-b;

a=1,b=3
a=a^b;
b=a^b;
a=a^b;

判断奇偶数：

a=4,b=5
a&1==0?"偶数":"奇数";
b&1==0?"偶数":"奇数";

30.只出现一次的数字：异或^

题目：

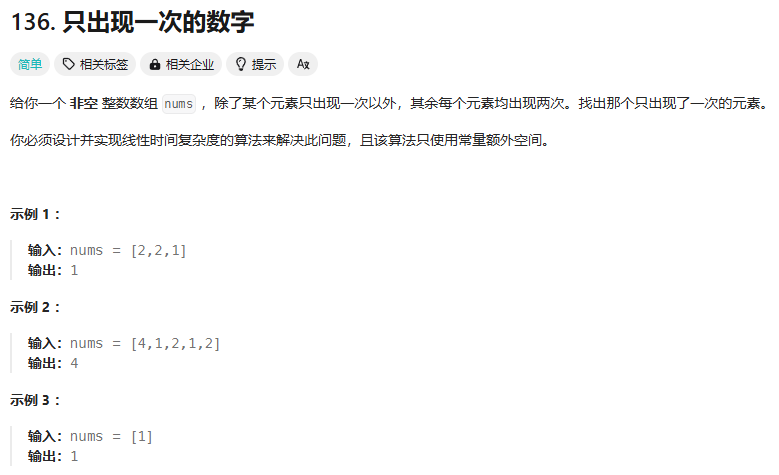
思路：

题目只有一个数字只出现一次，其他数字都只出现两次，就可以用^来解决，

因为同一个数异或自己就等于0,0异或一个数还是那个数本身，所以我们依次都异或一遍，最后得出的数就是

只出现一次的数

异或：

class Solution {
    public int singleNumber(int[] nums) {
        int res=0;
        for(int num:nums){
            res=res^num;
        }
        return res;
    }
}

31.比特位计数：位运算，N的二进制中1的个数=[N&(N-1)]这个数字1的个数+1

题目：

题解：

位运算，N的二进制中1的个数=[N&(N-1)]这个数字1的个数+1

很难懂：

class Solution {
    public int[] countBits(int n) {
        int[] nums=new int[n+1];
        for(int i=1;i<=n;i++){
            nums[i]=nums[i&(i-1)]+1;
        }
        return nums;
    }
}

利用奇偶数判断：

class Solution {
    public int[] countBits(int n) {
        int[] nums=new int[n+1];
        for(int i=1;i<=n;i++){
            nums[i]= ((i&1)==1?nums[i-1]+1:nums[i>>1]);
        }
        return nums;
    }
}

刘梦杰自己写，易懂一点：

class Solution {
    public int[] countBits(int n) {
        int[] nums=new int[n+1];
        for(int i=0;i<=n;i++){
            int count=0;
            int j=i;
            while(j!=0){
                j=j&(j-1);
                count++;
            }
            nums[i]=count;
        }
        return nums;
    }
}

32.汉明距离：位运算异或^

题目：

思路：

结合31题：

异或：

class Solution {
    public int hammingDistance(int x, int y) {
        int xor=x^y;
        int n=0;
        while(xor!=0){
            xor=xor&(xor-1);
            n++;
        }
        return n;
    }
}

33.有效的括号：栈

解题：

class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack=new Stack<Character>();
        char[] arr=s.toCharArray();
        for(char a:arr){
            if(a=='('){
                stack.push(')');
            }else if(a=='{'){
                stack.push('}');
            }else if(a=='['){
                stack.push(']');
            }else{
                if(stack.isEmpty() || stack.pop()!=a){
                    return false;
                }
            }
        }
        if(!stack.isEmpty()) return false;
        return true;
    }
}

34.字符串相加：双指针

题目：

双指针：

class Solution {
    public String addStrings(String num1, String num2) {
        int t=0;
        StringBuilder res = new StringBuilder("");
        for(int i=num1.length()-1,j=num2.length()-1;i>=0 || j>=0;i--,j--){
            int n1=(i>=0)?num1.charAt(i)-'0':0;
            int n2=(j>=0)?num2.charAt(j)-'0':0;
            res.append((n1+n2+t)%10);
            t=(n1+n2+t)/10;
        }
        if(t==1){
            res.append(1);
        }
        return res.reverse().toString();
    }
}

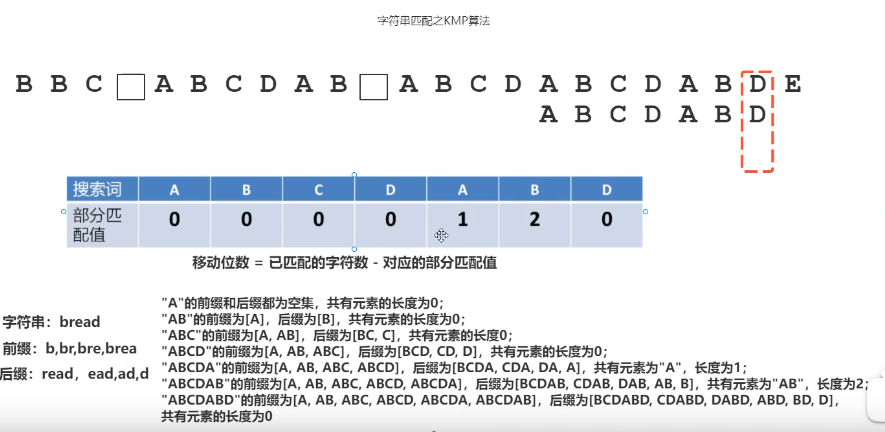
特别篇：字符串匹配BM算法和KMP算法

BM算法：

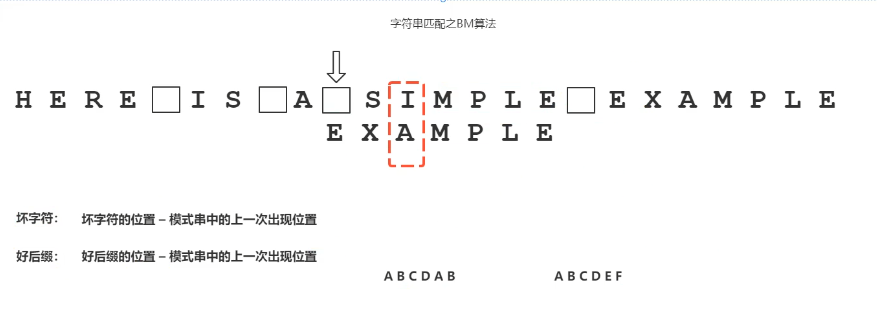
KPM算法：

35.最大子数组和：动态规划

题目：

解题：

动态规划（更清晰易懂）：

class Solution {
    public int maxSubArray(int[] nums) {
        //动态规划
        int[] dp=new int[nums.length];
        dp[0]=nums[0];
        int max=nums[0];
        for(int i=1;i<nums.length;i++){
            dp[i]=Math.max(nums[i],dp[i-1]+nums[i]);
            if(max<dp[i]){
                max=dp[i];
            }
        }
        return max;
    }
}

优化改良版动态规划：

class Solution {
    public int maxSubArray(int[] nums) {
        int cur = 0;
        int result = Integer.MIN_VALUE;
        for (int i = 0; i < nums.length; i++) {
            cur += nums[i];
            result = Math.max(cur,result);
            if(cur < 0) cur = 0;
        }
        return result;
    }
}

36.买卖股票的最佳时机：记录+遍历

思路：

每次都假设是今天卖出，然后求今天之前的历史最低点与今天的差价，记录最大差价。

记录+遍历：

class Solution {
    public int maxProfit(int[] prices) {
        if(prices==null) return 0;
        int maxProfit=0;
        int minPrice=prices[0];
        for(int i=0;i<prices.length;i++){
            int todayProfit=prices[i]-minPrice;
            if(todayProfit>maxProfit){
                maxProfit=todayProfit;
            }
            if(minPrice>prices[i]){
                minPrice=prices[i];
            }
        }
        return maxProfit;
    }
}

37.用 Rand7() 实现 Rand10()：

题目：

思路：

代码：

class Solution extends SolBase {
    public int rand10() {
        int rand=(rand7()-1)*7+rand7();
        while(rand>40){
            rand=(rand7()-1)*7+rand7();
        }
        return rand%10+1;
    }
}

38.搜索插入位置：二分查找

题目：

解题：

二分查找：

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        while(left<=right){
            int mid=(left+right)/2;
            if(nums[mid]>target){
                right=mid-1;
            }else if(nums[mid]<target){
                left=mid+1;
            }else{
                return mid;
            }
        }
        return left;
    }
}

39.杨辉三角

题目：

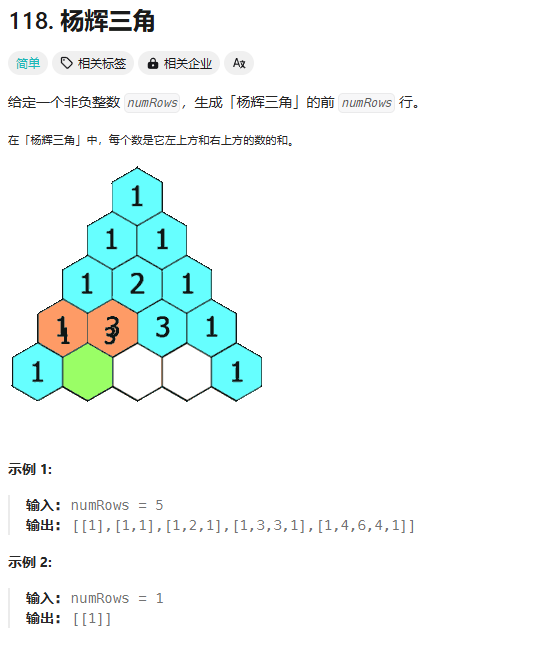
思路：

代码：

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> result=new ArrayList<List<Integer>>(numRows);
        result.add(List.of(1));
        for(int i=1;i<numRows;i++){
            List<Integer> list=new ArrayList<Integer>(i+1);
            list.add(1);
            for(int j=1;j<i;j++){
                list.add(result.get(i-1).get(j-1)+result.get(i-1).get(j));
            }
            list.add(1);
            result.add(list);
        }
        return result;
    }
}

40.多数元素：摩尔投票

题目：

思路：

抵消原则

摩尔投票，设众数和票数

遍历数组，每当票数被抵消为0时设当前数字为众数，然后票数+1，往后遇到不同的数票数就-1,直到票数为0重新此步骤，最后留下来的众数就是多数元素

摩尔投票：

class Solution {
    public int majorityElement(int[] nums) {
        int zz=nums[0];//众数
        int count=0;//票数
        for(int n:nums){
            if(count==0){
                zz=n;
            }
            if(n==zz){
                count+=1;
            }else{
                count-=1;
            }
        }
        return zz;
    }
}

41.移除元素：双指针

题目：

思路：

27.移除元素-暴力解法

双指针：

class Solution {
    public int removeElement(int[] nums, int val) {
        int slow=0;
        for(int i=0;i<nums.length;i++){
            if(nums[i]!=val){
                nums[slow]=nums[i];
                slow++;
            }
        }
        return slow;
    }
}

42.有序数组的平方：双指针

题目：

思路：

双指针：

class Solution {
    public int[] sortedSquares(int[] nums) {
        int left=0;
        int right=nums.length-1;
        int index=nums.length-1;
        int[] res=new int[nums.length];
        while(left<=right){
            int l=nums[left]*nums[left];
            int r=nums[right]*nums[right];
            if(l>r){
                left++;
                res[index]=l;
                index--;
            }else{
                right--;
                res[index]=r;
                index--;
            }
        }
        return res;
    }
}

43.长度最小的子数组：前后双指针(滑动窗口)

题目：

思路：

前后双指针代替队列：

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int left=0;
        int right=0;
        int min=Integer.MAX_VALUE;
        int sum=0;
        while(right<nums.length){
            sum+=nums[right++];
            while(sum>=target){//把前面的数一个一个退出判断sum还大不大于target
                min=Math.min(min,right-left);
                sum-=nums[left];
                left++;
            }
        }
        return min == Integer.MAX_VALUE ? 0 : min;
    }
}

44.特殊数组2

题目：

代码：

a[]数组存两个数字中间的逗号记录左右两边的数是否奇偶性一致，然后累加，最后判断两个下标的a是否相等，若相等则表示下标中的一段数字都是奇偶性不一致的，所以都是累加0，所以相等，所以返回true

class Solution {
    public boolean[] isArraySpecial(int[] nums, int[][] queries) {
        int[] a=new int[nums.length];
        boolean[] ans=new boolean[queries.length];
        for(int i=1;i<nums.length;i++){
            if(nums[i]%2==nums[i-1]%2){
                a[i]=a[i-1]+1;
            }
            else{
                a[i]=a[i-1]+0;
            }
        }
        for(int j=0;j<queries.length;j++){
            ans[j]=a[queries[j][0]]==a[queries[j][1]];
        }
        return ans;
    }
}

45.删除有序数组中的重复项：快慢指针

题目：

思路：

快指针元素等于慢指针元素，快指针后移，快指针元素不等于慢指针元素，慢指针先后移再覆盖为快指针元素，然后快指针后移

另一种说法：（慢指针相当于新数组的遍历，快指针来遍历原数组，只有当快指针元素没有重复时候，慢指针才会后移并写入未重复元素）

快慢指针：

class Solution {
    public int removeDuplicates(int[] nums) {
        int fast=0;
        int slow=0;
        while(fast<nums.length){
            if(nums[fast]!=nums[slow]){
                slow++;
                nums[slow]=nums[fast];
            }
            fast++;
        }
        return slow+1;
    }
}

46.将有序数组转换成二叉搜索数：递归

题目：

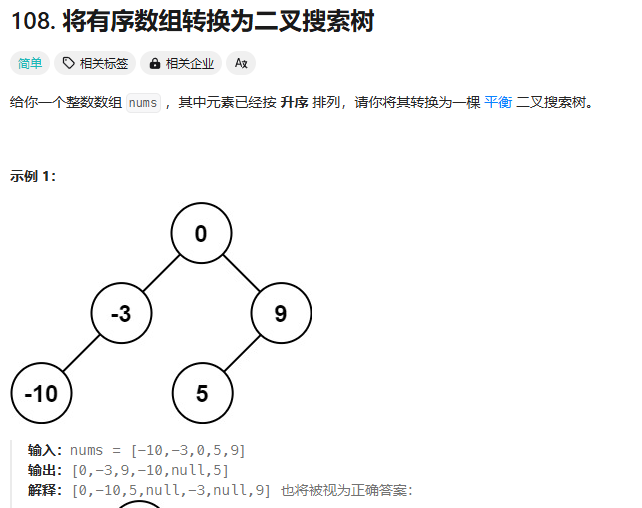
思路：

中序遍历，root选有序数组的最中间的元素，然后递归造左右子树

递归：

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        int left=0;
        int right=nums.length-1;
        return createTree(nums,left,right);
    }

    private TreeNode createTree(int[] nums,int left,int right){
        if(left>right) return null;
        int mid=(left+right)/2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left=createTree(nums,left,mid-1);
        root.right=createTree(nums,mid+1,right);
        return root;
    }
}

47.无重复字符的最长子串：滑动窗口

题目：

思路：

其实就是一个队列,比如例题中的 abcabcbb，进入这个队列（窗口）为 abc 满足题目要求，当再进入 a，队列变成了 abca，这时候不满足要求。所以，我们要移动这个队列！

如何移动？

我们只要把队列的左边的元素移出就行了，直到满足题目要求！

滑动窗口：

class Solution {
    public int lengthOfLongestSubstring(String s) {
        int max=0;
        int left=0;
        HashMap<Character,Integer> map=new HashMap<Character,Integer>();
        for(int i=0;i<s.length();i++){
            if(map.containsKey(s.charAt(i))){
                left=Math.max(left,map.get(s.charAt(i)) + 1);
            }
            map.put(s.charAt(i),i);
            max=Math.max(i-left+1,max);
        }
        return max;
    }
}

48.二叉树的直径：递归

题目：

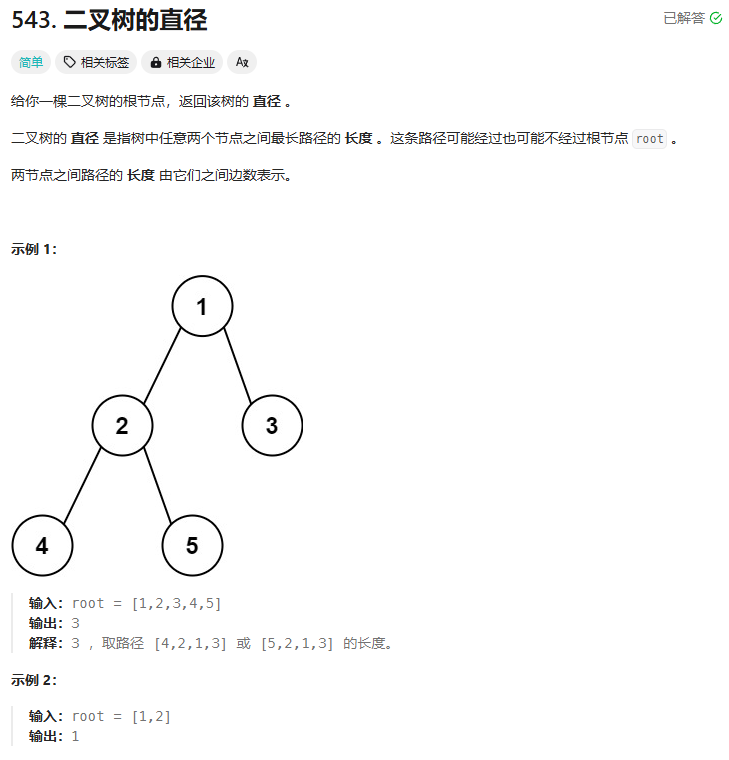
递归：

class Solution {
    private int ans;

    public int diameterOfBinaryTree(TreeNode root) {
        dfs(root);
        return ans;
    }

    private int dfs(TreeNode root){
        if(root==null){
            return -1;
        }
        int left=dfs(root.left)+1;
        int right=dfs(root.right)+1;
        ans=Math.max(ans,left+right);
        return Math.max(left,right);
    }
}

49.跳跃游戏：贪心算法

题目：

思路：

从头到尾遍历数组一遍，算出每个位置能到达的最远位置记录到max里，如果max大于数组最后一个下标则表示可以到达，如果中途遍历的i大于了最远到达长度表示卡在一个地方了不能到达最后一个下标

贪心算法：

//标准题解：
public class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;
        int rightmost = 0;
        for (int i = 0; i < n; ++i) {
            if (i <= rightmost) {
                rightmost = Math.max(rightmost, i + nums[i]);
                if (rightmost >= n - 1) {
                    return true;
                }
            }
        }
        return false;
    }
}

//刘梦杰题解：
class Solution {
    public boolean canJump(int[] nums) {
        int max=0;
        for(int i=0;i<nums.length;i++){
            if(i>max){
                return false;
            }
            max=(max>i+nums[i]?max:i+nums[i]);
            if(max>=nums.length-1){
                return true;
            }
        }
        return false;
    }
}

50.员工的重要性：哈希表+DFS

哈希表+DFS：

class Solution {
    public int getImportance(List<Employee> employees, int id) {
        Map<Integer, Employee> employeeMap = new HashMap<>(employees.size());
        for (Employee e : employees) {
            employeeMap.put(e.id, e);
        }
        return dfs(employeeMap, id);
    }

    private int dfs(Map<Integer, Employee> employeeMap, int id) {
        Employee e = employeeMap.get(id);
        int res = e.importance;
        for (int subId : e.subordinates) {
            res += dfs(employeeMap, subId);
        }
        return res;
    }
}

1.两数求和：哈希映射

2.判断子序列：双指针

3.回文数：字符串反转(慢) 双指针(略慢) 数字处理/%(快)

4.加一：数学解题%

5.爬楼梯：斐波那契数列(递归+hashmap，循环)

6.合并两个有序数组：双指针

7.移动零：双指针

8.找到所有数组中消失的数字：

9.合并两有序链表：双指针，递归

10.删除排序链表中的重复元素：正常遍历和递归

11.环形链表：快慢指针

12.环形链表2 ：快慢指针

13.相交链表：双指针交错遍历

14.反转链表：双指针

15.回文链表：快慢指针+反转链表

16.链表的中间节点：快慢指针

17.链表中倒数第k个节点：双指针 前后指针

18.找出与数组相加的整数1：最小值之差

19.用栈模拟队列：两个栈

20.字符串解码：栈

21.二叉树中序遍历：递归

22.二叉树前序遍历：递归

23.二叉树后序遍历：递归

24.对称二叉树：递归

25.二叉树的最大深度：递归

26.平衡二叉树：递归+最大深度

27.翻转二叉树：递归

特别篇：十大排序算法

28.手撕快速排序：

28.2 手撕归并排序：

29.二分查找：循环,递归

特别篇：原码反码补码和位运算

30.只出现一次的数字：异或^

31.比特位计数：位运算，N的二进制中1的个数=[N&(N-1)]这个数字1的个数+1

32.汉明距离：位运算异或^

33.有效的括号：栈

34.字符串相加：双指针

特别篇：字符串匹配BM算法和KMP算法

35.最大子数组和：动态规划

36.买卖股票的最佳时机：记录+遍历

37.用 Rand7() 实现 Rand10()：

38.搜索插入位置：二分查找

39.杨辉三角

40.多数元素：摩尔投票

41.移除元素：双指针

42.有序数组的平方：双指针

43.长度最小的子数组：前后双指针(滑动窗口)

44.特殊数组2

45.删除有序数组中的重复项：快慢指针

46.将有序数组转换成二叉搜索数：递归

47.无重复字符的最长子串：滑动窗口

48.二叉树的直径：递归

49.跳跃游戏：贪心算法

50.员工的重要性：哈希表+DFS

17.链表中倒数第k个节点：双指针前后指针